personal/compute-constrained-bayes
1
0
Fork 0
Code Issues Pull Requests Packages Projects Releases Wiki Activity

Compare commits

base: personal:00619aa0fba29ad302e72c1e2c12efcb452a9d6c
Branches Tags
personal:master
...
compare: personal:50deb4ef89b2f1c1a719d518736969537e61157d
Branches Tags
personal:master

4 Commits
00619aa0fb ... 50deb4ef89

Author SHA1 Message Date
NunoSempere
50deb4ef89 save copy of results. 2023-05-25 16:47:40 -07:00
NunoSempere
240f1294ca feat: improve README. 2023-05-25 16:38:36 -07:00
NunoSempere
c92d46ed92 fix: miniInfraBayes with interleaved sequence errors. 2023-05-25 15:39:50 -07:00
NunoSempere
ef34fb34fa step: add second infrabayesianism step. 2023-05-25 15:14:21 -07:00
7 changed files with 697 additions and 35 deletions
Show Stats Expand all files Collapse all files

91
README.md
View File

@ -3,7 +3,7 @@ Models of Bayesian-like updating under constrained compute
This repository contains some implementations of models of bayesian-like updating under constrained compute. The world in which these models operate is the set of sequences from the [Online Encyclopedia of Integer Sequences](https://oeis.org/), which can be downloaded from [here](https://oeis.org/wiki/JSON_Format,_Compressed_Files).
![](./screenshots/jit-bayes.png)
![](./outputs/jit-bayes.png)
## Models
@ -23,15 +23,58 @@ As described [here](https://nunosempere.com/blog/2023/02/04/just-in-time-bayesia
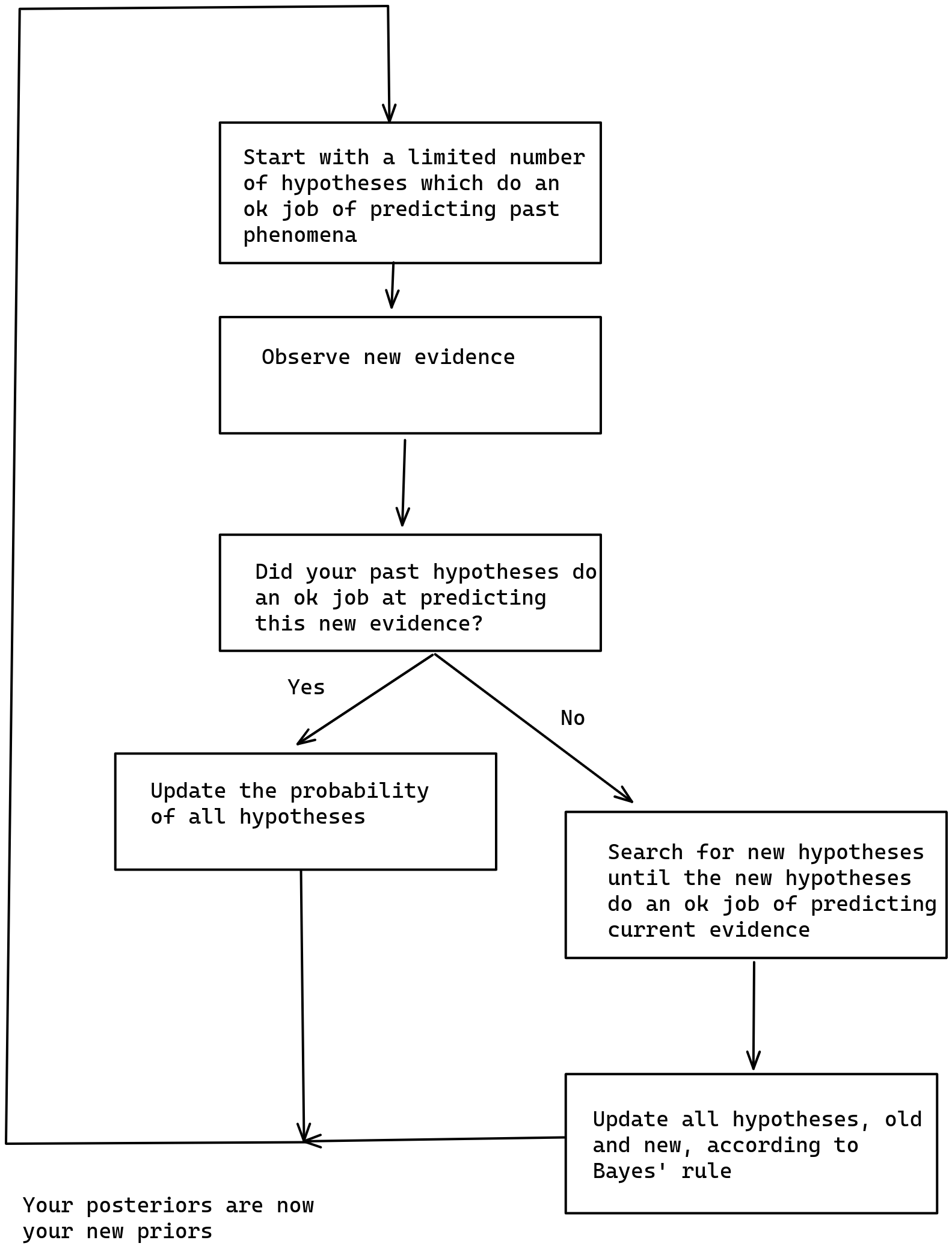
![](https://images.nunosempere.com/blog/2023/02/04/just-in-time-bayesianism/bayes-jit.png)
I think that the implementation here provides some value in terms of making fuzzy concepts explicit. For example, instead of "did your past hypotheses do an ok job at predicting this new evidence", I have code which looks at whether past predictions included the correct completion, and which expand the search for hypotheses if not.
I think that the implementation here provides some value in terms of making fuzzy concepts explicit. For example, instead of "did your past hypotheses do an ok job at predicting this new evidence", I have code which looks at whether past predictions included the correct completion, and which expands the search for hypotheses if not.
I later elaborated on this type of scheme on [A computable version of Solomonoff induction](https://nunosempere.com/blog/2023/03/01/computable-solomonoff/).
### Infrabayesianism
Mini-infrabayesianism part I
Caveat for this section: This represents my partial understanding of some parts of infrabayesianism, and ideally I'd want someone to check it. Errors may exist.
- Mini-infrabayesianism part II:
#### Part I: Infrabayesianism in the sense of producing a deterministic policy that maximizes worst-case utility (minimizes worst-case loss)
In this example:
- environments are the possible OEIS sequences, shown one element at a time
- the actions are observing some elements, and making predictions about what the next element will be condition
- loss is the sum of the log scores after each observation.
- Note that at some point you arrive at the correct hypothesis, and so your subsequent probabilities are 1.0 (100%), and your subsequent loss 0 (log(1))
Claim: If there are n sequences which start with s, and m sequences that start with s and continue with q, the action which minimizes loss is assigning a probability of m/n to completion q.
Proof: In this case, let #{xs} denote the number of OEIS sequences that start with sequence xs, and let ø denote the empty sequence, such that ${ø} is the total number of OEIS sequences. Then your loss for a sequence (e1, e2, ..., en)—where en is the element by which you've identified the sequence with certainty—is log(#{e1}/#{ø}) + log(#{e1e2}/#{e1}) + ... + log(#{e1...en}/#{e1...e(n-1)}). Because log(a) + log(b) = log(a×b), that simplifies to log(#{e1...en}/#{ø}). But there is one unique sequence which starts with e1...en, and hence #{e1...en} = 1. Therefore this procedure just assigns the same probability to each sequence, namely 1/(number of sequences).
Now suppose you have some policy that makes predictions that deviate from the above, i.e., you assign a different probability than 1/#{} to some sequence. Then there is some sequence to which you are assigning a lower probability. Hence the maximum loss is higher. Therefore the policy which minimizes loss is the one described above.
Note: In the infrabayesianism post, the authors look at some extension of expected values which allow us to compute the minmax. But in this case, the result of policies in an environment is deterministic, and we can compute the minmax directly.
Note: To some extent having the result of policies in an environment be deterministic, and also the same in all environments, defeats a bit of the point of infrabayesianism. So I see this step as building towards a full implementation of Infrabayesianism.
#### Part II: Infrabayesianism in the additional sense of having hypotheses only over parts of the environment, without representing the whole environment
Have the same scheme as in Part I, but this time the environment is two OEIS sequences interleaved together.
Some quick math: If one sequence represented as an ASCII string is 4 Kilobytes (obtained with `du -sh data/line`), and the whole of OEIS takes 70MB, then all possibilities for two OEIS sequences interleaved together is 70MB/4K * 70MB, or over 1 TB.
But you can imagine more mischevous environments, like: a1, a2, b1, a3, b2, c1, a4, b3, c2, d1, a4, b4, c3, d2, ..., or in triangular form:
```
a1,
a2, b1,
a3, b2, c1,
a4, b3, c2, d1,
a4, b4, c3, d2, ...
```
(where (ai), (bi), etc. are independently drawn OEIS sequences)
Then you can't represent this environment with any amount of compute, and yet by only having hypotheses over different positions, you can make predictions about what the next element will be when given a list of observations.
We are not there yet, but interleaving OEIS sequences already provides an example of this sort.
#### Part III: Capture some other important aspect of infrabayesianism (e.g., non-deterministic environments)
[To do]
## Built with
@ -44,26 +87,33 @@ Why nim? Because it is nice to use and [freaking fast](https://github.com/NunoSe
### Prerequisites
Install [nim](https://nim-lang.org/install.html) and make.
### Compilation
Install [nim](https://nim-lang.org/install.html) and make. Then:
```
git clone https://git.nunosempere.com/personal/compute-constrained-bayes.git
cd compute-constrained-bayes
cd src
make deps ## get dependencies
```
### Compilation
```
make fast ## also make, or make build, for compiling it with debug info.
./compute-constrained-bayes
```
### Alternatively:
See [here](./outputs/aha.html) for a copy of the program's outputs.
## Contributions
Contributions are very welcome, particularly around:
- [ ] Making the code more nim-like, using nim's standard styles and libraries
- [ ] Adding another example which is not logloss minimization for infrabayesianism
- [ ]
- [ ] Adding another example which is not logloss minimization for infrabayesianism?
- [ ] Adding other features of infrabayesianism?
## Roadmap
@ -79,30 +129,9 @@ Contributions are very welcome, particularly around:
- [x] Add the loop of: start with some small number of sequences, and if these aren't enough, read more.
- [x] Clean-up
- [ ] Infrabayesianism
- [ ] Infrabayesianism x1: Predicting interleaved sequences.
- [x] Infrabayesianism x1: Predicting interleaved sequences.
- Yeah, actually, I think this just captures an implicit assumption of Bayesianism as actually practiced.
- [x] Infrabayesianism x2: Deterministic game of producing a fixed deterministic prediction, and then the adversary picking whatever minimizes your loss
- I am actually not sure of what the procedure is exactly for computing that loss. Do you minimize over subsequent rounds of the game, or only for the first round? Look this up.
- [ ] Also maybe ask for help from e.g., Alex Mennen?
- [x] Lol, minimizing loss for the case where your utility is the logloss is actually easy.
---
An implementation of Infrabayesianism over OEIS sequences.
<https://oeis.org/wiki/JSON_Format,_Compressed_Files>
Or "Just-in-Time bayesianism", where getting a new hypothesis = getting a new sequence from OEIS which has the numbers you've seen so far.
Implementing Infrabayesianism as a game over OEIS sequences. Two parts:
1. Prediction over interleaved sequences. I choose two OEIS sequences, and interleave them: a1, b1, a2, b2.
- Now, you don't have hypothesis over the whole set, but two hypothesis over the
- I could also have a chemistry like iteration:
a1
a2 b1
a3 b2 c1
a4 b3 c2 d1
a5 b4 c3 d2 e1
.................
- And then it would just be computationally absurd to have hypotheses over the whole
2. Game where: You provide a deterministic procedure for estimating the probability of each OEIS sequence giving a list of trailing examples.

1
data/line Normal file
View File

@ -0,0 +1 @@
A000015 ,1,2,3,4,5,7,7,8,9,11,11,13,13,16,16,16,17,19,19,23,23,23,23,25,25,27,27,29,29,31,31,32,37,37,37,37,37,41,41,41,41,43,43,47,47,47,47,49,49,53,53,53,53,59,59,59,59,59,59,61,61,64,64,64,67,67,67,71,71,71,71,73,

572
outputs/aha.html Normal file
View File

@ -0,0 +1,572 @@
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<!-- This file was created with the aha Ansi HTML Adapter. https://github.com/theZiz/aha -->
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<meta http-equiv="Content-Type" content="application/xml+xhtml; charset=UTF-8" />
<title>stdin</title>
</head>
<body>
<pre>
$ unbuffer make run | aha > aha.html
./compute_constrained_bayes --verbosity:0
## Full prediction with access to all hypotheses (~Solomonoff)
## Initial sequence: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;]
continuation_probabilities=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;4&quot;</span>, <span style="color:blue;">0.5031144781144781</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.1727272727272727</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;6&quot;</span>, <span style="color:blue;">0.07878787878787878</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2&quot;</span>, <span style="color:blue;">0.0505050505050505</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;3&quot;</span>, <span style="color:blue;">0.04882154882154882</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;7&quot;</span>, <span style="color:blue;">0.02803030303030303</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1&quot;</span>, <span style="color:blue;">0.02474747474747475</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8&quot;</span>, <span style="color:blue;">0.02163299663299663</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;9&quot;</span>, <span style="color:blue;">0.01060606060606061</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;10&quot;</span>, <span style="color:blue;">0.009175084175084175</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.008838383838383838</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;12&quot;</span>, <span style="color:blue;">0.008501683501683501</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;16&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;14&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;0&quot;</span>, <span style="color:blue;">0.003282828282828283</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;15&quot;</span>, <span style="color:blue;">0.00260942760942761</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;13&quot;</span>, <span style="color:blue;">0.002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">0.001262626262626263</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;23&quot;</span>, <span style="color:blue;">0.000925925925925926</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;24&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;22&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;41&quot;</span>, <span style="color:blue;">0.0007575757575757576</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;28&quot;</span>, <span style="color:blue;">0.0006734006734006734</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.0005892255892255892</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;211&quot;</span>, <span style="color:blue;">0.0005050505050505051</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;30&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;26&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;35&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;25&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;4567&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-2&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-1&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-4&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;40&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;60&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;32&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;81&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;64&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;38&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;56&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;33&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;69&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;27&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;39&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;128&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;130&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;55&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;47&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;65&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;74&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;83&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;92&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;124&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;36&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;789&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2436&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;401&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;58&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;34&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;107&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;380&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-3&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;119&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;456&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8787&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;48&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;127&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;469&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;57&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;85&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;617&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-16&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1080&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;72&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;95&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;101&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;661&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;37&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2310&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;62&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;111213&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;44&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;99&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1767&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123543&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;173&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;21&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;42&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;144689999986441&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;54&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;512&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;371&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;52&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>)
]
## Predictions with increasingly many hypotheses
Showing predictions with increasingly many hypotheses after seeing @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;]
Predictions with 10% of the hypotheses
predictions=@[]
Predictions with 20% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.5</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.5</span>)]
Predictions with 30% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.3333333333333333</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.3333333333333333</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.3333333333333333</span>)]
Predictions with 40% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.25</span>)]
Predictions with 50% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.25</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.25</span>)]
Predictions with 60% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.2</span>)]
Predictions with 70% of the hypotheses
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.2</span>), <span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.2</span>)]
Predictions with 80% of the hypotheses
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.125</span>)
]
Predictions with 90% of the hypotheses
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.125</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.125</span>)
]
Predictions with 100% of the hypotheses
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">0.09090909090909091</span>)
]
## Prediction with limited number of hypotheses (~JIT-Bayes)
### Prediction after seeing 3 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;4&quot;</span>, <span style="color:blue;">0.375</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.25</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;6&quot;</span>, <span style="color:blue;">0.2083333333333333</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8&quot;</span>, <span style="color:blue;">0.04166666666666666</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;10&quot;</span>, <span style="color:blue;">0.04166666666666666</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;3&quot;</span>, <span style="color:blue;">0.04166666666666666</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;7&quot;</span>, <span style="color:blue;">0.04166666666666666</span>)
]
Correct continuation, 23 not found in set of hypotheses of size 1000/362901. Increasing size of the set of hypotheses.
Correct continuation, 23 not found in set of hypotheses of size 31000/362901. Increasing size of the set of hypotheses.
Increased number of hypotheses to 61000, and found 1 concordant hypotheses. Continuing
### Prediction after seeing 4 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation, 11 not found in set of hypotheses of size 61000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 91000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 121000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 151000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 181000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 211000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 241000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 271000/362901. Increasing size of the set of hypotheses.
Correct continuation, 11 not found in set of hypotheses of size 301000/362901. Increasing size of the set of hypotheses.
Increased number of hypotheses to 331000, and found 1 concordant hypotheses. Continuing
### Prediction after seeing 5 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 18
It was assigned a probability of 1.0
### Prediction after seeing 6 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;77&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 77
It was assigned a probability of 1.0
### Prediction after seeing 7 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;, &quot;77&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;46&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 46
It was assigned a probability of 1.0
### Prediction after seeing 8 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;, &quot;77&quot;, &quot;46&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;84&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 84
It was assigned a probability of 1.0
## Mini-infra-bayesianism over environments, where your utility in an environment is just the log-loss in the predictions you make until you become certain that you are in that environment.
### Prediction after seeing 3 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;4&quot;</span>, <span style="color:blue;">0.5031144781144781</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.1727272727272727</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;6&quot;</span>, <span style="color:blue;">0.07878787878787878</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2&quot;</span>, <span style="color:blue;">0.0505050505050505</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;3&quot;</span>, <span style="color:blue;">0.04882154882154882</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;7&quot;</span>, <span style="color:blue;">0.02803030303030303</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1&quot;</span>, <span style="color:blue;">0.02474747474747475</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8&quot;</span>, <span style="color:blue;">0.02163299663299663</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;9&quot;</span>, <span style="color:blue;">0.01060606060606061</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;10&quot;</span>, <span style="color:blue;">0.009175084175084175</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.008838383838383838</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;12&quot;</span>, <span style="color:blue;">0.008501683501683501</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;16&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;14&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;0&quot;</span>, <span style="color:blue;">0.003282828282828283</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;15&quot;</span>, <span style="color:blue;">0.00260942760942761</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;13&quot;</span>, <span style="color:blue;">0.002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">0.001262626262626263</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;23&quot;</span>, <span style="color:blue;">0.000925925925925926</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;24&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;22&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;41&quot;</span>, <span style="color:blue;">0.0007575757575757576</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;28&quot;</span>, <span style="color:blue;">0.0006734006734006734</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.0005892255892255892</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;211&quot;</span>, <span style="color:blue;">0.0005050505050505051</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;30&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;26&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;35&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;25&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;4567&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-2&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-1&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-4&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;40&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;60&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;32&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;81&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;64&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;38&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;56&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;33&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;69&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;27&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;39&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;128&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;130&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;55&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;47&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;65&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;74&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;83&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;92&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;124&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;36&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;789&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2436&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;401&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;58&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;34&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;107&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;380&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-3&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;119&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;456&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8787&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;48&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;127&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;469&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;57&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;85&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;617&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-16&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1080&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;72&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;95&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;101&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;661&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;37&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2310&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;62&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;111213&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;44&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;99&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1767&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123543&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;173&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;21&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;42&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;144689999986441&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;54&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;512&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;371&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;52&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>)
]
Correct continuation was 23
It was assigned a probability of 0.000925925925925926
And hence a loss of -6.984716320118265
Total loss is: -6.984716320118265
### Prediction after seeing 4 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">0.09090909090909091</span>)
]
Correct continuation was 11
It was assigned a probability of 0.09090909090909091
And hence a loss of -2.397895272798371
Total loss is: -9.382611592916636
### Prediction after seeing 5 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 18
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -9.382611592916636
### Prediction after seeing 6 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;77&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 77
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -9.382611592916636
### Prediction after seeing 7 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;, &quot;77&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;46&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 46
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -9.382611592916636
### Prediction after seeing 8 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;3&quot;, &quot;23&quot;, &quot;11&quot;, &quot;18&quot;, &quot;77&quot;, &quot;46&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;84&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 84
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -9.382611592916636
## Mini-infra-bayesianism over environments, where your utility in an environment is just the log-loss in the predictions you make until you become certain that you are in that environment. This time with a twist: You don't have hypotheses over the sequences you observe, but rather over their odd and even position, i.e., you think that you observe interleaved OEIS sequences, (a1, b1, a2, b2, a3, b3). See the README.md for more.
### Prediction after seeing 6 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;4&quot;</span>, <span style="color:blue;">0.5031144781144781</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.1727272727272727</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;6&quot;</span>, <span style="color:blue;">0.07878787878787878</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2&quot;</span>, <span style="color:blue;">0.0505050505050505</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;3&quot;</span>, <span style="color:blue;">0.04882154882154882</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;7&quot;</span>, <span style="color:blue;">0.02803030303030303</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1&quot;</span>, <span style="color:blue;">0.02474747474747475</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8&quot;</span>, <span style="color:blue;">0.02163299663299663</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;9&quot;</span>, <span style="color:blue;">0.01060606060606061</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;10&quot;</span>, <span style="color:blue;">0.009175084175084175</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.008838383838383838</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;12&quot;</span>, <span style="color:blue;">0.008501683501683501</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;16&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;14&quot;</span>, <span style="color:blue;">0.003787878787878788</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;0&quot;</span>, <span style="color:blue;">0.003282828282828283</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;15&quot;</span>, <span style="color:blue;">0.00260942760942761</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;13&quot;</span>, <span style="color:blue;">0.002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">0.001262626262626263</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.001178451178451178</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;23&quot;</span>, <span style="color:blue;">0.000925925925925926</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;24&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;22&quot;</span>, <span style="color:blue;">0.0008417508417508417</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;41&quot;</span>, <span style="color:blue;">0.0007575757575757576</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;28&quot;</span>, <span style="color:blue;">0.0006734006734006734</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.0005892255892255892</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;211&quot;</span>, <span style="color:blue;">0.0005050505050505051</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;30&quot;</span>, <span style="color:blue;">0.0004208754208754209</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;26&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;35&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;25&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;4567&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-2&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-1&quot;</span>, <span style="color:blue;">0.0003367003367003367</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-4&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;40&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;60&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;32&quot;</span>, <span style="color:blue;">0.0002525252525252525</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;81&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;64&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;38&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;56&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;33&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;69&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;27&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;39&quot;</span>, <span style="color:blue;">0.0001683501683501684</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;128&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;130&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;55&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;47&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;65&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;74&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;83&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;92&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;124&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;36&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;789&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2436&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;401&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;58&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;34&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;107&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;380&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-3&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;119&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;456&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;8787&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;48&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;127&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;469&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;57&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;85&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;617&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;-16&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1080&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;72&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;95&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;101&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;661&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;37&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;2310&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;62&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;111213&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;44&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;99&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;1767&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;123543&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;173&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;21&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;42&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;144689999986441&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;54&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;512&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;371&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;52&quot;</span>, <span style="color:blue;">8.417508417508418e-05</span>)
]
Correct continuation was 23
It was assigned a probability of 0.000925925925925926
And hence a loss of -6.984716320118265
Total loss is: -6.984716320118265
### Prediction after seeing 7 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.4035087719298245</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.1228070175438596</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;23&quot;</span>, <span style="color:blue;">0.1228070175438596</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.07017543859649122</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.07017543859649122</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;24&quot;</span>, <span style="color:blue;">0.03508771929824561</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;7&quot;</span>, <span style="color:blue;">0.03508771929824561</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;101&quot;</span>, <span style="color:blue;">0.03508771929824561</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;41&quot;</span>, <span style="color:blue;">0.03508771929824561</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;47&quot;</span>, <span style="color:blue;">0.01754385964912281</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20&quot;</span>, <span style="color:blue;">0.01754385964912281</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;22&quot;</span>, <span style="color:blue;">0.01754385964912281</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;25&quot;</span>, <span style="color:blue;">0.01754385964912281</span>)
]
Correct continuation was 23
It was assigned a probability of 0.1228070175438596
And hence a loss of -2.097141118779237
Total loss is: -9.081857438897501
### Prediction after seeing 8 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;49&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;323&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;17&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;20880467999847912034355032910540&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;19&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;5&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;11&quot;</span>, <span style="color:blue;">0.09090909090909091</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;43&quot;</span>, <span style="color:blue;">0.09090909090909091</span>)
]
Correct continuation was 11
It was assigned a probability of 0.09090909090909091
And hence a loss of -2.397895272798371
Total loss is: -11.47975271169587
### Prediction after seeing 9 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;]
predictions=@[
<span style="color:teal;"></span>(<span style="color:green;">&quot;29&quot;</span>, <span style="color:blue;">0.2857142857142857</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;41&quot;</span>, <span style="color:blue;">0.2857142857142857</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;37&quot;</span>, <span style="color:blue;">0.1428571428571428</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;31&quot;</span>, <span style="color:blue;">0.1428571428571428</span>),
<span style="color:teal;"></span>(<span style="color:green;">&quot;47&quot;</span>, <span style="color:blue;">0.1428571428571428</span>)
]
Correct continuation was 47
It was assigned a probability of 0.1428571428571428
And hence a loss of -1.945910149055313
Total loss is: -13.42566286075118
### Prediction after seeing 10 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;18&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 18
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 11 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;59&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 59
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 12 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;77&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 77
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 13 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;, &quot;77&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;71&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 71
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 14 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;, &quot;77&quot;, &quot;71&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;46&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 46
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 15 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;, &quot;77&quot;, &quot;71&quot;, &quot;46&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;83&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 83
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 16 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;, &quot;77&quot;, &quot;71&quot;, &quot;46&quot;, &quot;83&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;84&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 84
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
### Prediction after seeing 17 observations: @[&quot;1&quot;, &quot;2&quot;, &quot;2&quot;, &quot;11&quot;, &quot;3&quot;, &quot;13&quot;, &quot;23&quot;, &quot;23&quot;, &quot;11&quot;, &quot;47&quot;, &quot;18&quot;, &quot;59&quot;, &quot;77&quot;, &quot;71&quot;, &quot;46&quot;, &quot;83&quot;, &quot;84&quot;]
predictions=@[<span style="color:teal;"></span>(<span style="color:green;">&quot;107&quot;</span>, <span style="color:blue;">1.0</span>)]
Correct continuation was 107
It was assigned a probability of 1.0
And hence a loss of 0.0
Total loss is: -13.42566286075118
</pre>
</body>
</html>

3
outputs/aha.sh Normal file
View File

@ -0,0 +1,3 @@
unbuffer make run | aha > aha.html
# where aha is https://github.com/theZiz/aha

0
screenshots/jit-bayes.png → outputs/jit-bayes.png
View File

Side by Side Swipe Overlay

Before

Width:  |  Height:  |  Size: 153 KiB

After

Width:  |  Height:  |  Size: 153 KiB

BIN
src/compute_constrained_bayes
View File

Binary file not shown.

65
src/compute_constrained_bayes.nim
View File

@ -163,7 +163,7 @@ proc jitBayesLoop(
## Infrabayesianism
proc miniInfraBayes(
proc miniInfraBayesArgminMaxLoss(
seqs: seq[seq[string]],
observations: seq[string],
n_observations_seen: int,
@ -192,11 +192,64 @@ proc miniInfraBayes(
echo "And hence a loss of ", new_loss
echo "Total loss is: ", foldl(losses, a + b, 0.0)
proc getEvens(xs: seq[string]): seq[string] =
var evens: seq[string]
for i,x in xs:
if i mod 2 == 0:
evens.add(x)
return evens
## Infrabayesianism. Part 1: Have hypotheses over just part of the world.
proc getOdds(xs: seq[string]): seq[string] =
var odds: seq[string]
for i,x in xs:
if i mod 2 == 1:
odds.add(x)
return odds
proc interleave(xs: seq[string], ys: seq[string]): seq[string] =
if xs.len != ys.len:
echo "Interleaved sequences have to have the same length; returning empty sequence."
return @[]
else:
var zs: seq[string]
for i in 0..<xs.len:
zs.add(xs[i])
zs.add(ys[i])
return zs
## Infrabayesianism. Part 2: Take the infimum over the possible loss.
proc miniInfraBayesArgminMaxLossInterleavedHypotheses(
seqs: seq[seq[string]],
observations: seq[string],
n_observations_seen: int,
utility_function: string
) =
if utility_function != "logloss":
echo "miniInfraBayes function only programmed for the logloss utility function"
return
else:
echo "## Mini-infra-bayesianism over environments, where your utility in an environment is just the log-loss in the predictions you make until you become certain that you are in that environment. This time with a twist: You don't have hypotheses over the sequences you observe, but rather over their odd and even position, i.e., you think that you observe interleaved OEIS sequences, (a1, b1, a2, b2, a3, b3). See the README.md for more."
var losses: seq[float]
for i in n_observations_seen..<observations.len:
var parity_subsequence: seq[string]
if i mod 2 == 0:
parity_subsequence = getEvens(observations[0..<i])
else:
parity_subsequence = getOdds(observations[0..<i])
let predictions = predictContinuation(seqs, parity_subsequence)
echo "### Prediction after seeing ", i, " observations: ", observations[0..<i]
print predictions
let correct_continuation = observations[i]
let considered_continuations = predictions.map(prediction => getHypothesis(prediction))
let correct_continuation_index = findIndex(considered_continuations, correct_continuation)
let p_correct_continuation = getProbability(predictions[correct_continuation_index])
let new_loss = ln(p_correct_continuation)
losses.add(new_loss)
echo "Correct continuation was ", correct_continuation
echo "It was assigned a probability of ", p_correct_continuation
echo "And hence a loss of ", new_loss
echo "Total loss is: ", foldl(losses, a + b, 0.0)
## Display outputs
echo ""
@ -220,5 +273,9 @@ jitBayesLoop(seqs, observations, 3, 1_000, 30_000)
echo ""
observations = @["1", "2", "3", "23", "11", "18", "77", "46", "84"]
miniInfraBayes(seqs, observations, 3, "logloss")
miniInfraBayesArgminMaxLoss(seqs, observations, 3, "logloss")
echo ""
observations = interleave(@["1", "2", "3", "23", "11", "18", "77", "46", "84"], @["2", "11", "13", "23", "47", "59", "71", "83", "107"])
miniInfraBayesArgminMaxLossInterleavedHypotheses(seqs, observations, 6, "logloss")
echo ""