feat: improve README.
This commit is contained in:
parent
c92d46ed92
commit
240f1294ca
76
README.md
76
README.md
|
|
@ -23,15 +23,58 @@ As described [here](https://nunosempere.com/blog/2023/02/04/just-in-time-bayesia
|
|||
|
||||
|
||||
|
||||
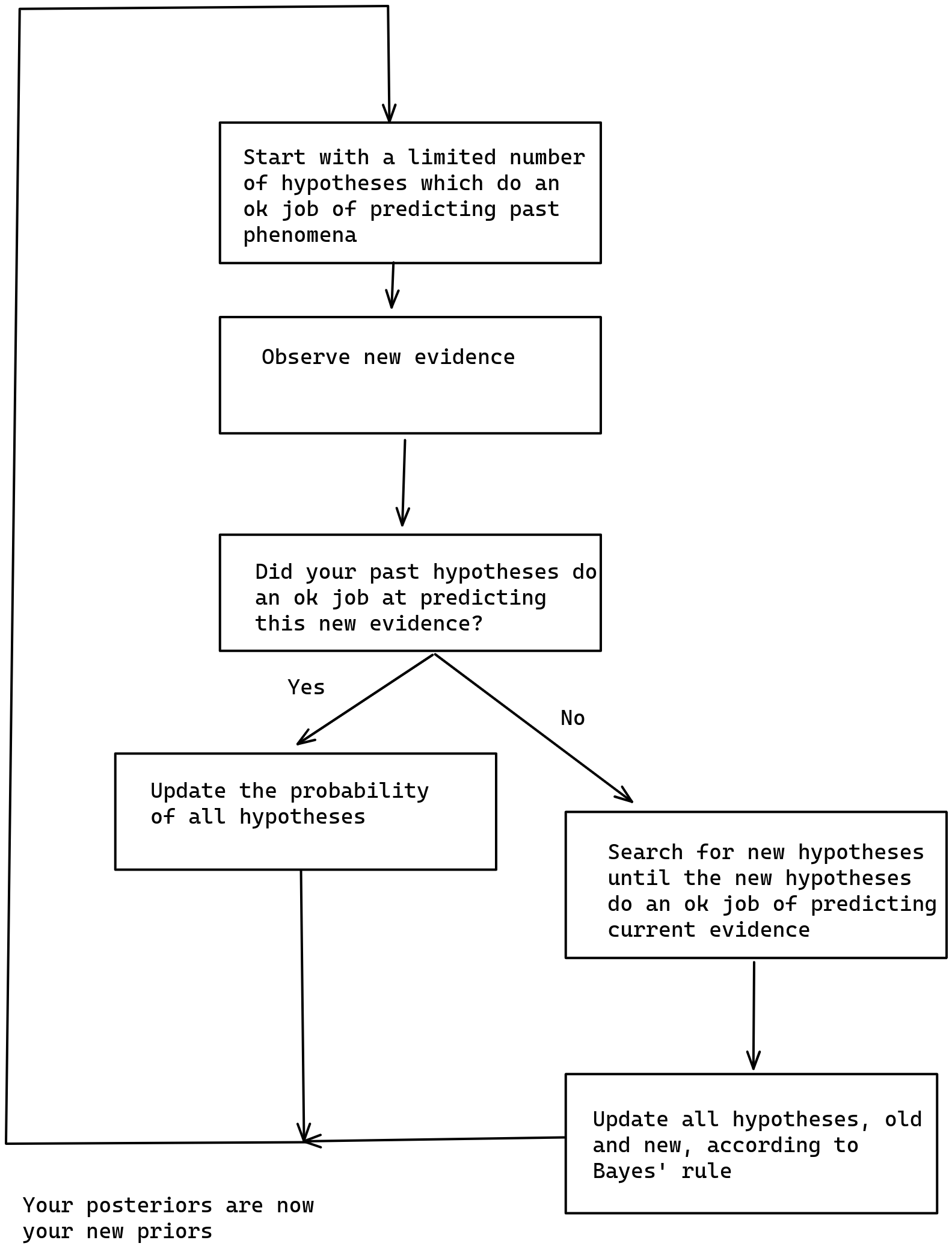
I think that the implementation here provides some value in terms of making fuzzy concepts explicit. For example, instead of "did your past hypotheses do an ok job at predicting this new evidence", I have code which looks at whether past predictions included the correct completion, and which expand the search for hypotheses if not.
|
||||
I think that the implementation here provides some value in terms of making fuzzy concepts explicit. For example, instead of "did your past hypotheses do an ok job at predicting this new evidence", I have code which looks at whether past predictions included the correct completion, and which expands the search for hypotheses if not.
|
||||
|
||||
I later elaborated on this type of scheme on [A computable version of Solomonoff induction](https://nunosempere.com/blog/2023/03/01/computable-solomonoff/).
|
||||
|
||||
### Infrabayesianism
|
||||
|
||||
Mini-infrabayesianism part I
|
||||
Caveat for this section: This represents my partial understanding of some parts of infrabayesianism, and ideally I'd want someone to check it. Errors may exist.
|
||||
|
||||
- Mini-infrabayesianism part II:
|
||||
#### Part I: Infrabayesianism in the sense of producing a deterministic policy that maximizes worst-case utility (minimizes worst-case loss)
|
||||
|
||||
In this example:
|
||||
|
||||
- environments are the possible OEIS sequences, shown one element at a time
|
||||
- the actions are observing some elements, and making predictions about what the next element will be condition
|
||||
- loss is the sum of the log scores after each observation.
|
||||
- Note that at some point you arrive at the correct hypothesis, and so your subsequent probabilities are 1.0 (100%), and your subsequent loss 0 (log(1))
|
||||
|
||||
Claim: If there are n sequences which start with s, and m sequences that start with s and continue with q, the action which minimizes loss is assigning a probability of m/n to completion q.
|
||||
|
||||
Proof: In this case, let #{xs} denote the number of OEIS sequences that start with sequence xs, and let ø denote the empty sequence, such that ${ø} is the total number of OEIS sequences. Then your loss for a sequence (e1, e2, ..., en)—where en is the element by which you've identified the sequence with certainty—is log(#{e1}/#{ø}) + log(#{e1e2}/#{e1}) + ... + log(#{e1...en}/#{e1...e(n-1)}). Because log(a) + log(b) = log(a×b), that simplifies to log(#{e1...en}/#{ø}). But there is one unique sequence which starts with e1...en, and hence #{e1...en} = 1. Therefore this procedure just assigns the same probability to each sequence, namely 1/(number of sequences).
|
||||
|
||||
Now suppose you have some policy that makes predictions that deviate from the above, i.e., you assign a different probability than 1/#{} to some sequence. Then there is some sequence to which you are assigning a lower probability. Hence the maximum loss is higher. Therefore the policy which minimizes loss is the one described above.
|
||||
|
||||
Note: In the infrabayesianism post, the authors look at some extension of expected values which allow us to compute the minmax. But in this case, the result of policies in an environment is deterministic, and we can compute the minmax directly.
|
||||
|
||||
Note: To some extent having the result of policies in an environment be deterministic, and also the same in all environments, defeats a bit of the point of infrabayesianism. So I see this step as building towards a full implementation of Infrabayesianism.
|
||||
|
||||
#### Part II: Infrabayesianism in the additional sense of having hypotheses only over parts of the environment, without representing the whole environment
|
||||
|
||||
Have the same scheme as in Part I, but this time the environment is two OEIS sequences interleaved together.
|
||||
|
||||
Some quick math: If one sequence represented as an ASCII string is 4 Kilobytes (obtained with `du -sh data/line`), and the whole of OEIS takes 70MB, then all possibilities for two OEIS sequences interleaved together is 70MB/4K * 70MB, or over 1 TB.
|
||||
|
||||
But you can imagine more mischevous environments, like: a1, a2, b1, a3, b2, c1, a4, b3, c2, d1, a4, b4, c3, d2, ..., or in triangular form:
|
||||
|
||||
```
|
||||
a1,
|
||||
a2, b1,
|
||||
a3, b2, c1,
|
||||
a4, b3, c2, d1,
|
||||
a4, b4, c3, d2, ...
|
||||
```
|
||||
|
||||
(where (ai), (bi), etc. are independently drawn OEIS sequences)
|
||||
|
||||
Then you can't represent this environment with any amount of compute, and yet by only having hypotheses over different positions, you can make predictions about what the next element will be when given a list of observations.
|
||||
|
||||
We are not there yet, but interleaving OEIS sequences already provides an example of this sort.
|
||||
|
||||
#### Part III: Capture some other important aspect of infrabayesianism (e.g., non-deterministic environments)
|
||||
|
||||
[To do]
|
||||
|
||||
## Built with
|
||||
|
||||
|
|
@ -62,8 +105,8 @@ make fast ## also make, or make build, for compiling it with debug info.
|
|||
Contributions are very welcome, particularly around:
|
||||
|
||||
- [ ] Making the code more nim-like, using nim's standard styles and libraries
|
||||
- [ ] Adding another example which is not logloss minimization for infrabayesianism
|
||||
- [ ]
|
||||
- [ ] Adding another example which is not logloss minimization for infrabayesianism?
|
||||
- [ ] Adding other features of infrabayesianism?
|
||||
|
||||
## Roadmap
|
||||
|
||||
|
|
@ -79,30 +122,9 @@ Contributions are very welcome, particularly around:
|
|||
- [x] Add the loop of: start with some small number of sequences, and if these aren't enough, read more.
|
||||
- [x] Clean-up
|
||||
- [ ] Infrabayesianism
|
||||
- [ ] Infrabayesianism x1: Predicting interleaved sequences.
|
||||
- [x] Infrabayesianism x1: Predicting interleaved sequences.
|
||||
- Yeah, actually, I think this just captures an implicit assumption of Bayesianism as actually practiced.
|
||||
- [x] Infrabayesianism x2: Deterministic game of producing a fixed deterministic prediction, and then the adversary picking whatever minimizes your loss
|
||||
- I am actually not sure of what the procedure is exactly for computing that loss. Do you minimize over subsequent rounds of the game, or only for the first round? Look this up.
|
||||
- [ ] Also maybe ask for help from e.g., Alex Mennen?
|
||||
- [x] Lol, minimizing loss for the case where your utility is the logloss is actually easy.
|
||||
|
||||
---
|
||||
|
||||
An implementation of Infrabayesianism over OEIS sequences.
|
||||
<https://oeis.org/wiki/JSON_Format,_Compressed_Files>
|
||||
|
||||
Or "Just-in-Time bayesianism", where getting a new hypothesis = getting a new sequence from OEIS which has the numbers you've seen so far.
|
||||
|
||||
Implementing Infrabayesianism as a game over OEIS sequences. Two parts:
|
||||
1. Prediction over interleaved sequences. I choose two OEIS sequences, and interleave them: a1, b1, a2, b2.
|
||||
- Now, you don't have hypothesis over the whole set, but two hypothesis over the
|
||||
- I could also have a chemistry like iteration:
|
||||
a1
|
||||
a2 b1
|
||||
a3 b2 c1
|
||||
a4 b3 c2 d1
|
||||
a5 b4 c3 d2 e1
|
||||
.................
|
||||
- And then it would just be computationally absurd to have hypotheses over the whole
|
||||
|
||||
2. Game where: You provide a deterministic procedure for estimating the probability of each OEIS sequence giving a list of trailing examples.
|
||||
|
|
|
|||
Loading…
Reference in New Issue
Block a user