| data | ||
| screenshots | ||
| src | ||
| .gitignore | ||
| README.md | ||
Models of Bayesian-like updating under constrained compute
This repository contains some implementations of models of bayesian-like updating under constrained compute. The world in which these models operate is the set of sequences from the Online Encyclopedia of Integer Sequences, which can be downloaded from here.
Models
Given the start of a sequence of integers, what is the probability of possible completions? This post offers various answers:
Unconstrained prediction
Just look at all possible sequence, and assign a probability to each continuation based on its frequency across all sequences
Prediction with access to subsequently more hypotheses.
Look at 10%, 20%,..., 80%, 90%, 100% of sequences, and give the probability of each continuation based on its frequencies across n% of sequences
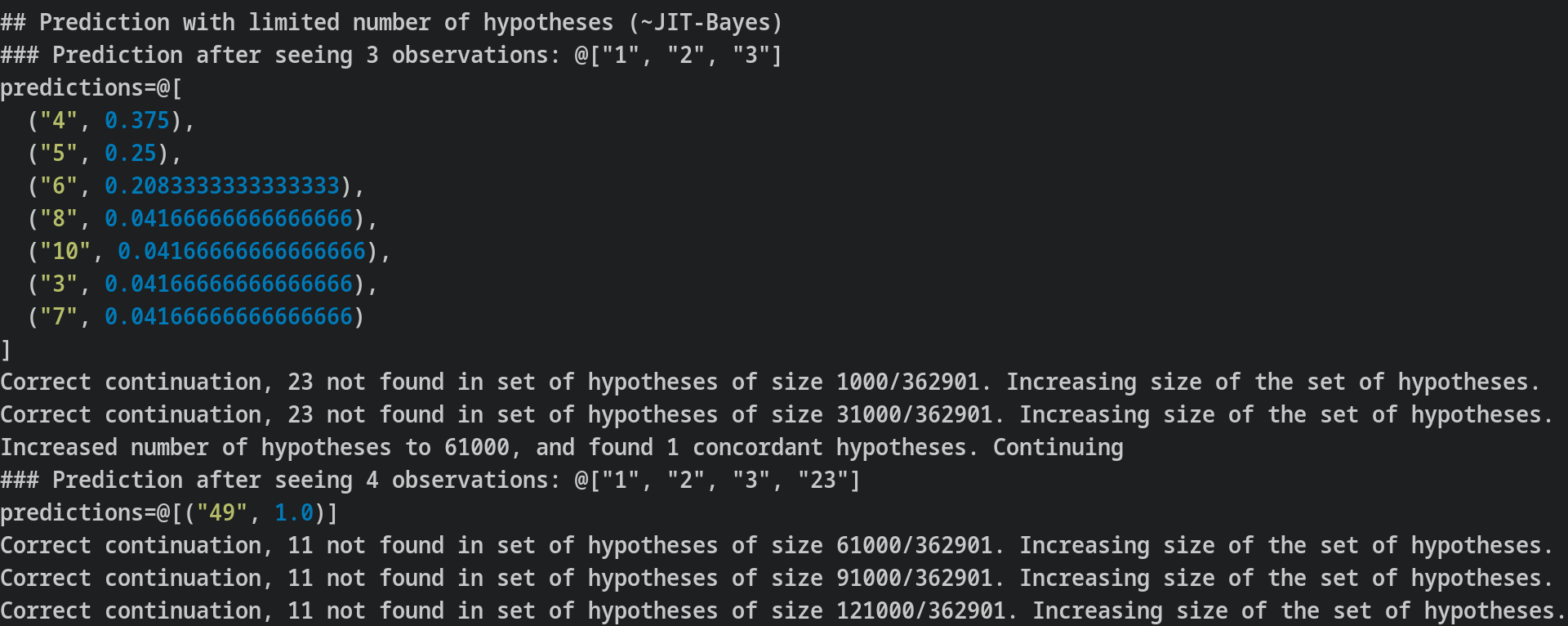
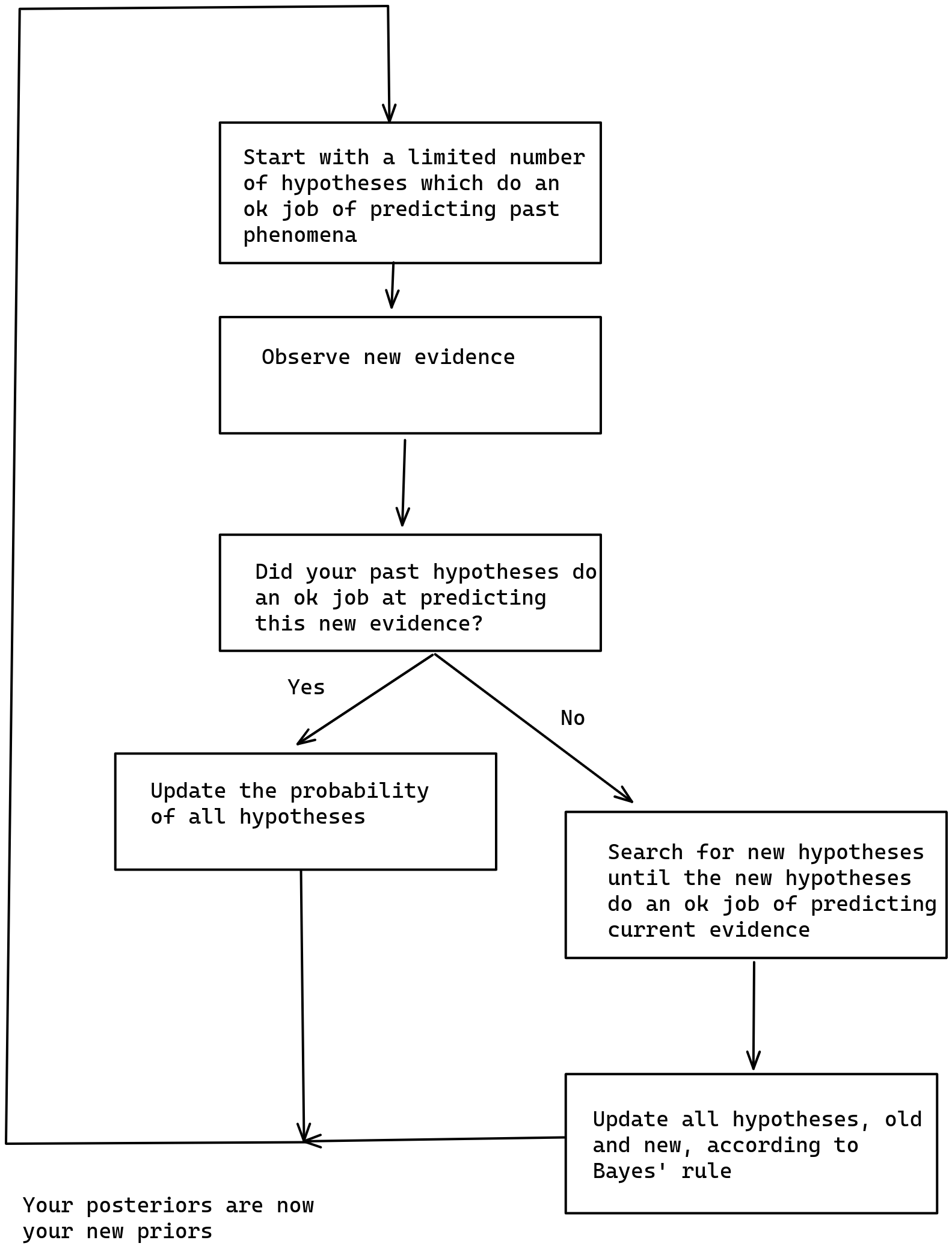
Just in time Bayesianism
As described here, Just-in-time bayesianism is this scheme:
I think that the implementation here provides some value in terms of making fuzzy concepts explicit. For example, instead of "did your past hypotheses do an ok job at predicting this new evidence", I have code which looks at whether past predictions included the correct completion, and which expand the search for hypotheses if not.
I later elaborated on this type of scheme on A computable version of Solomonoff induction.
Infrabayesianism
Mini-infrabayesianism part I
- Mini-infrabayesianism part II:
Built with
Why nim? Because it is nice to use and freaking fast.
Getting started
Prerequisites
Install nim and make.
Compilation
git clone https://git.nunosempere.com/personal/compute-constrained-bayes.git
cd compute-constrained-bayes
cd src
make deps ## get dependencies
make fast ## also make, or make build, for compiling it with debug info.
./compute-constrained-bayes
Contributions
Contributions are very welcome, particularly around:
- Making the code more nim-like, using nim's standard styles and libraries
- Adding another example which is not logloss minimization for infrabayesianism
Roadmap
- Exploration of OEIS data
- Subdivide subsequent tasks into steps
- Simple prediction of the next integer
- Simple predictions v1
- Wrangle the return types to something semi-elegant
- [-] Maybe add some caching, e.g., write continuations to file, and read them next time.
- JIT Bayesianism:
- Function to predict with a variable number of hypotheses
- Function to start predicting with a small number of hypotheses, and get more if the initial ones aren't enough.
- Add the loop of: start with some small number of sequences, and if these aren't enough, read more.
- Clean-up
- Infrabayesianism
- Infrabayesianism x1: Predicting interleaved sequences.
- Yeah, actually, I think this just captures an implicit assumption of Bayesianism as actually practiced.
- Infrabayesianism x2: Deterministic game of producing a fixed deterministic prediction, and then the adversary picking whatever minimizes your loss
- I am actually not sure of what the procedure is exactly for computing that loss. Do you minimize over subsequent rounds of the game, or only for the first round? Look this up.
- Also maybe ask for help from e.g., Alex Mennen?
- Lol, minimizing loss for the case where your utility is the logloss is actually easy.
- Infrabayesianism x1: Predicting interleaved sequences.
- Simple prediction of the next integer
An implementation of Infrabayesianism over OEIS sequences. https://oeis.org/wiki/JSON_Format,_Compressed_Files
Or "Just-in-Time bayesianism", where getting a new hypothesis = getting a new sequence from OEIS which has the numbers you've seen so far.
Implementing Infrabayesianism as a game over OEIS sequences. Two parts:
- Prediction over interleaved sequences. I choose two OEIS sequences, and interleave them: a1, b1, a2, b2.
- Now, you don't have hypothesis over the whole set, but two hypothesis over the
- I could also have a chemistry like iteration: a1 a2 b1 a3 b2 c1 a4 b3 c2 d1 a5 b4 c3 d2 e1 .................
- And then it would just be computationally absurd to have hypotheses over the whole
- Game where: You provide a deterministic procedure for estimating the probability of each OEIS sequence giving a list of trailing examples.