8.5 KiB
Planteamiento. Explicación cultivada en Wikipedia.
Podemos modelizar el problema poblacional de encontrar una pareja aceptando las asunciones de El problema de las parejas estables (Stable Marriage Problem). Estas son: que la población se divide en hombres y mujeres, y que todo hombre y toda mujer prefieren a los individuos del sexo opuesto en un orden concreto.
Por supuesto, la población es plenamente heterosexual. Además, nadie tiene estándares, es decir, todos prefieren mejor estar mal acompañados que estar solos. A pesar de estas asunciones, me sigue pareciendo interesante presentar qué pasa si se sigue el siguiente algoritmo:
En la iteración 1,
a) Cada hombre no emparejado se declara a la mujer que más prefiere
b) Cada mujer dice "tal vez" al pretendiente que más prefiere y "no" a los demás.
En la iteración n+1 / n+1 > 1
a) Cada hombre que todavía no está emparejado se acerca a la mujer que más prefiere de entre las que todavía no le han rechazado.
b) Cada mujer dice "tal vez" al nuevo pretendiente que más prefiere, si y solo si prefiere a este sobre su pareja actual. Si elige a alguien para reemplazar a su pareja, la expareja está ahora desemparejada y en la siguiente ronda participa en a).
Esto se repite hasta que todos quedan emparejados. Además, cuando el proceso se termine no existirá ninguna pareja {A,B} tal que A y B preferirían al otro sobre su pareja actual y no estén ya juntos. Esto pasa por razones fáciles de entender y que están fácilmente disponibles en Wikipedia
Un ejemplo
Si hay tres hombres, H1, H2 y H3, y tres mujeres M1, M2 y M3, representamos sus preferencias respectivamente por:
Preferencias(H1)={M1,M2,M3};
P(H2)={M2, M1,M3};
P(H3)= {M1, M3, M2}
P(M1) = {H1, H3, H2};
P(M2) = {H2, H1, H3};
P(M3) = {H1, H2, H3}
Esto "significa" que el H1 prefiere a la M1, luego a la M2, y finalmente a la M3, mientras que la M1 prefiere al H1 seguido del H3 y del H2.
Si se implementa el algoritmo,
Ronda 1) H1 -> (se declara a) M1; H2 -> M2; H3 -> M1. H1 y H2 son aceptados, H3 es rechazado.
Ronda 2) H3 -> M3. H3 es aceptado.
Fin.
Las parejas finales son {H1,M1}; {H2, M2}; {H3,M3}
Los Hs han terminado, de media, con su opción: (1 + 1 + 2) / 3 = 4 / 3, pues H1 termina con su primera opción, H2 también y H3 con su segunda.
Las Ms han terminado, de media, con su opción (1 + 1 + 3) / 3 = 5 / 3, pues M1 termina con su primera opción, M2 también y M3 con su tercera.
Nomenclatura: Podemos llamar a 4/3 la "distancia al ideal" de los Hs, y a 5 / 3 la "distancia al ideal" de las Ms. Cuanto más bajo es el número, mejor para ellos.
Fin del ejemplo
Dicho lo cual, Wikipedia menciona que el algoritmo descrito resulta óptimo para los pretendientes. Me interesa cuantificar esa afirmación anto para preferencias aleatorias y no aleatorias. Para ello, he escrito varios programas en Python, que se pueden acceder aquí. Incidentalmente, estimo que la complejidad del asunto es similar a la la chicha de este proyecto de fin de carrera: Algoritmo de Gale-Shapley. Variaciones y alternativas; Documento archivado, que trata de algo similar.
Resultados:
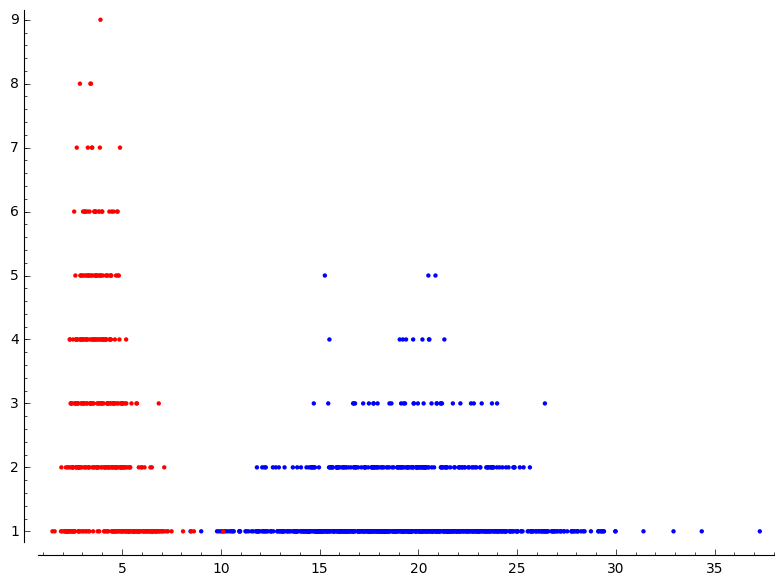
En las gráficas que siguen, un punto representa un nivel de "distancia al ideal" de un sexo, donde el rojo representa a los hombres y al azul a las mujeres. El que el punto esté más arriba implica que ese "nivel de distancia" es más común, y si está cerca del cero, que es menos frecuente. Frecuente entre el resultado final de preferencias inciales elegidas o bien aleatoriamente o bien cercanas un orden canónico. Si quisiéramos que todos fuesen felices, querríamos que los puntos estuviesen arriba a la izquierda. (Tal vez quieras leer este párrafo otra vez).
a) Preferencias elegidas aleatoriamente.
Para experimento con 20 personas de cada sexo, repetido 100 veces, obtenemos la siguiente gráfica✝:
Hay un patron, que se va discerniendo a medida que aumentamos el número de repeticiones.
Para 10^3 repeticiones:
Para 10^4 repeticiones:
Y para 2*10^4 repeticiones:
Para una población de 100 de cada sexo, obtenemos resultados similares.
Para 1000 repeticiones:
Y con una granularidad de 0.05 y 2000 repeticiones:
.png)
Y con una granularidad de 0,05 y 3000 repeticiones:
.png)
Para conseguir resultados "bonitos" podemos o bien reducir el número de personas o bien aumentar el número de experimentos. Si hacemos ambas cosas, con 10 sujetos de cada sexo y 2*10^4 experimentos, obtenemos lo siguiente:
b) Preferencias elegidas no aleatoriamente.
Modelamos el asunto de la siguiente manera: Hay una preferencia platónica [H1, H2 , H3, H4, H5,...], es decir, el hombre n es más deseable que el n+1, y lo mismo con las mujeres. Sobre esta lista platónica, los sujetos tienen un número variable de variaciones, donde una variación es intercambiar la persona n con la n+1. Daré la magnitud de la variación el % sobre la población, es decir, si hay n personas de cada sexo, v% variación se corresponde con floor(n.v/100) variaciones, donde floor(x) es el redondeo hacia abajo de x.
Es directo que para 0% variación la curva se corresponde con una campana centrada en n/2, donde n es la población✝✝.
Para un 10% de variación y 2000 repeticiones:
Para una población de 20 de cada sexo, obtenemos:
.png)
Y para una población de 100:
.png)
Y se ven por donde van los tiros. Como sabemos que estamos hablando de campanas más o menos de Gauss, podemos pasar a contemplar solamente la media, que será el eje de simetría de la campana. En la siguiente gráfica se muestran las medias de diferentes variaciones aplicadas a una población de 20 sujetos de cada sexo. Es un poco diferente:
El punto (a,b) representa dos medias de un experimento repetido 100 veces, donde a (eje x) es la media de los hombres y b (eje y) es la media de las mujeres. El color representa la variación; cuanto más azul, más variación. La variación va de 0% a 1000%, en intervalos de 20%.
Nótese que los ejes no están centrados. La línea azul es y=x, por lo que mayor azar (más variaciones) benefician a ambos sexos, pero más rápido a los hombres. Recordamos que para una población de preferencias aleatorias tendríamos puntos en torno al (2.12, 4.98), respectivamente la media de hombres y de mujeres.
El punto negro flotando por encima de la recta es la media de una población aleatoria.
Moraleja
La moraleja, no obstante, depende de en qué medida nuestras asunciones se cumplan en la realidad, y estas no son robustas. Es, entonces, una cuestión de criterio personal si una validez parcial de los principios implica una validez parcial de las conclusiones.
Dejo como ejercicio al lector y como preguntas a mí mismo:
¿Cuantas variaciones son necesarias para llegar a una lista decentemente pseudoaleatorio? ¿Qué pasa si solo hay un sexo, d.h., si todos son bisexuales? Demuestra que la existencia de una configuración estable de matrimonios está garantizada, o da un contraejemplo. ¿Se pueden construir casos patológicos en los que todos los hombres terminen con su última opción y todas las mujeres con su primera? N.B.: Parece que esto ya ha sido estudiado, véase Improving Man-Optimal Stable Matchings by Minimum Changeof Preference Lists, Takao Inoshita et al, extraído de: https://pdfs.semanticscholar.org/461c/aa254679c8834ac90cf12ea4cec625c3b16d.pdf Demuéstrese que las campanas de Gauss se van separando a medida que n aumenta. ¿A qué es proporcional esa separación? ✝ El lector perspicaz se habrá dado cuenta de que en las gráficas hay puntos en el intervalo [0,1]. Esto se debe a que, en Python, la primera posición de una lista es la posición cero. No se preocupen; réstenle 1 a los números utilizados en el ejemplo.
✝✝ Realmente (n-1)/2, porque el más deseado es el 0, no el 1. Pero da igual. Aunque ahora que lo pienso, tal vez tenga un error por uno (off by one error) en algún sitio.




.png)


