| .. | ||
| decision-method.png | ||
| index.js | ||
| package.json | ||
| README.md | ||
| tests.js | ||
About
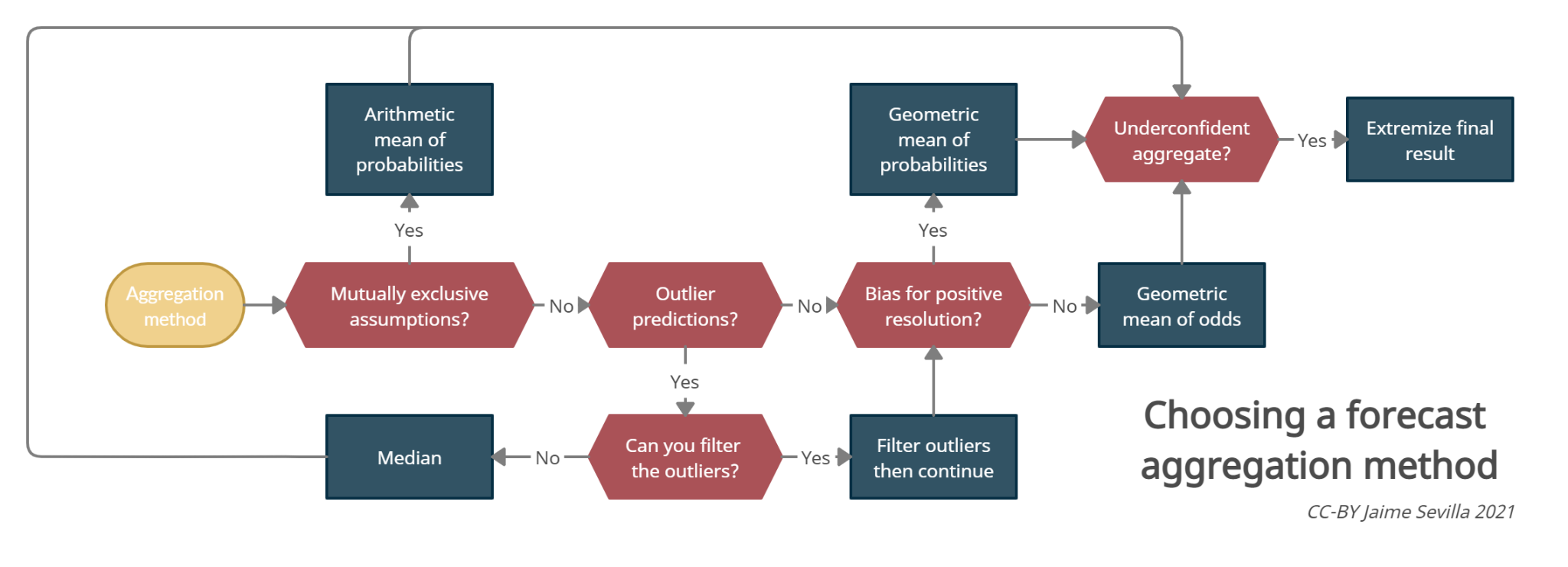
This package contains a series of utilities for forecast aggregation. It is currently in alpha, meaning that the code hasn't been tested much.
For an introduction to different aggregation methods, see Jaime Sevilla's Aggregation series. For an explanation of the neyman method, see here.
Built with
- vanilla javascript
- Best readme template
- lerna
Getting started
Installation
npm install @forecasting/aggregation
Usage
import {
median,
arithmeticMean,
geometricMean,
geometricMeanOfOdds,
extremizedGeometricMeanOfOdds,
neyman,
} from "@forecasting/aggregation";
let ps = [0.1, 0.2, 0.4, 0.5];
console.log(ps);
console.log(median(ps));
console.log(arithmeticMean(ps));
console.log(geometricMean(ps));
console.log(geometricMeanOfOdds(ps));
console.log(extremizedGeometricMeanOfOdds(ps, 1.5)); // 1.5 is the extremization factor
console.log(extremizedGeometricMeanOfOdds(ps, 2.5));
console.log(neyman(ps));
// invalid inputs, will return -1
let notArrayOfProbabilities0 = "Hello world!";
console.log(arithmeticMean(notArrayOfProbabilities0)); // -1
let notArrayOfProbabilities1 = [];
console.log(arithmeticMean(notArrayOfProbabilities1)); // -1
let notArrayOfProbabilities2 = ["a"];
console.log(arithmeticMean(notArrayOfProbabilities2)); // -1
let notArrayOfProbabilities3 = [2, 4, 5];
console.log(arithmeticMean(notArrayOfProbabilities3)); // -1
let notArrayOfProbabilities4 = [0.2, 4, 5];
console.log(arithmeticMean(notArrayOfProbabilities4)); // -1
const chosenAggregationMethod = neyman;
const getAggregatedProbabilities = (array) => {
let result = neyman(array);
if (result == -1) {
// handle case somehow; maybe throw an error, e.g.:
// throw new Error("Invalid array of probabilities")
} else {
return result;
}
};
Roadmap
- validate probability (must be 0<= p <=1)
- Decide on a return type if probabilities are not validated (-1? / null?)
- Write wrapper code for validation
- Validate that array.length > 0
- add weighting? by recency?
- filter outliers?